Seven Konigsberg Bridges
Let’s tackle the following puzzle below: Which of the figure below is impossible to be drawn either without lifting the pen from the paper or without tracing the same line more than once?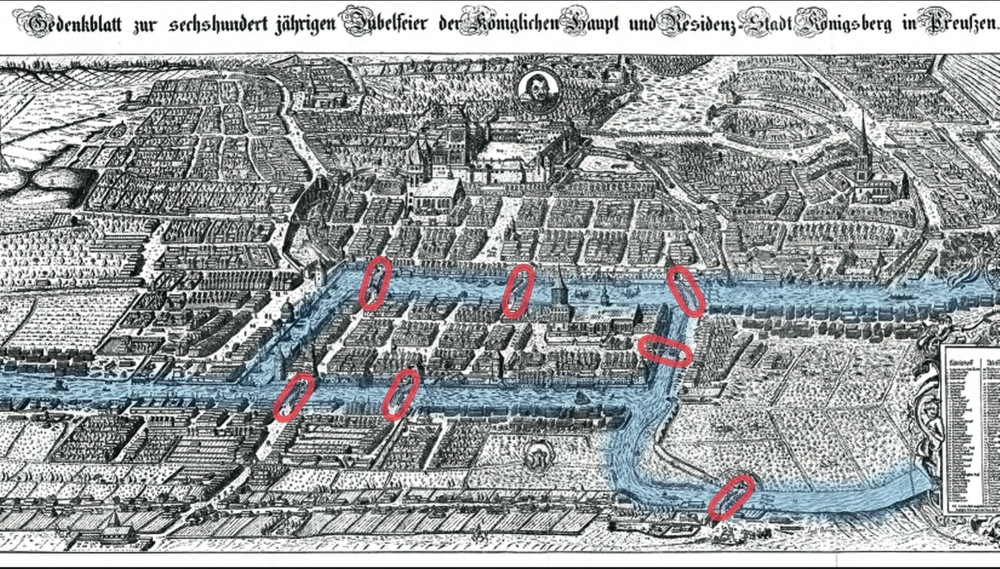
Figure 2:An old map depicting Königsberg,. The red lines circle the sevens bridges.
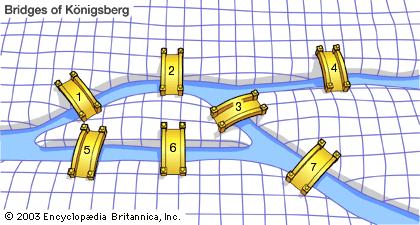
Figure 3: A simplified version of the map.
We can further simplify the map by taking the four lands in the picture as points. As such, the map can be reduced to a form that is much easier to work with, as shown below:
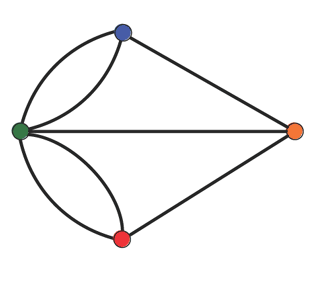
Figure 4: Our final simplified version of the map.
It looks familiar, right? Yes, it is familiar to the pictures in the previous question. So our question now is : how to traverse all lines on the map in a single trip?
Figure 5: Leonhard Euler(AD 1707-1873) was a Swiss mathematician, physicist, astronomer, logician and engineer who pioneered the development of several branches in mathematics, including infinitesimal calculus, graph theory, topology and analytic number theory.
Euler has proven it is impossible to traverse all lines in the mentioned map in a single trip.
To understand Leonhard Euler’s solution in a simple way, let us start with a point.

Figure 6
Any line traverses this point will yield another new line connected to the point as how the bridge is connected to the land.
.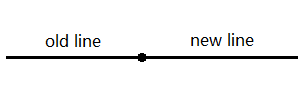
Figure 7
Equivalently, for any unicursal drawing, if the point is neither a starting point nor an ending point, numbers of lines(N) connected to this point will always be an even number, no matter how many lines has traversed it.
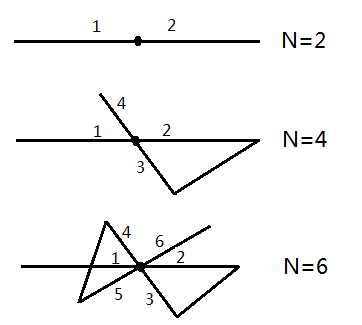
Figure 8
N is an odd number if and only if the point is the starting point or ending point.
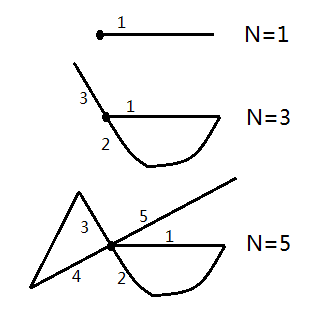
Figure 9
A point of which N is an odd number is known as an odd number point. In any unicursal(single trip) drawing, there are only two odd number points, which are the starting point and the ending point. Hence, it is impossible to draw a unicursal drawing which contains more than two odd number point. As what we saw in Figure 4, there are four odd number points in the map, which make it impossible to be drawn by using a unicursal line. In other words, It is impossible for us to find a way to traverse all 7 bridges in Konigsberg in a single trip, provided that we only travel on the lands and bridges. Back to our previous IQ question, by applying the same principle, we can easily deduce that picture C which has 4 odd number points cannot be drawn using a unicursal line. In the history of mathematics, Euler's solution of the Königsberg bridge problem is considered to lay down the foundation of graph theory and one of the first proofs in the theory of networks. In addition, Euler's recognition that the key information was the number of bridges and the list of their endpoints (rather than their exact positions) presaged the development of topology. Well, what is the use if we know the solution of the Konigsberg bridges? Any application of it? Here i will show you one.
Try another question!
Jordan is a paperboy. Every morning, the newspaper lorry will unload newspaper to his hostel. Jordan’s job is to deliver newspaper all along the streets(blue lines in figure 10) in the town he lives, and back to the newspaper office(“F” in figure 10 ) to make a report after he has finished his job. Suppose Jordan can choose a hostel to live among position A, B, C and D, which is the most convenient place for him to do his job?
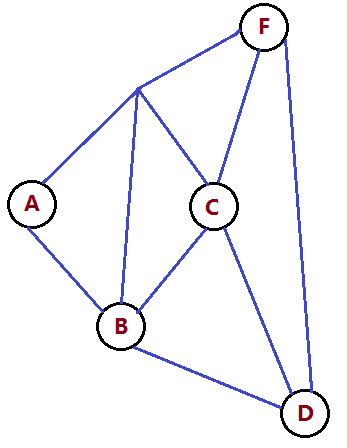
Figure 10
Since you have studied the solution of the konigsberg’s bridges, you can find the answer easily now, isn’t it?
