Small angle approximation
Ever wonder how those beautiful equations come from? \begin{equation} T=2\pi (\frac{l}{g}), n\lambda = \frac{ax}{D} \end{equation}
There are many ways we use to derive the equations, some were derived from very basic assumptions and basic algebras (cancellation, rearrangement), some were derived from higher level mathematics like L'Hospital's Rule . In A level, some equations can be derived without knowing advanced levels calculus or integrals. Now, we are going to explore one of the useful tools in derivation, namely, the small angle approximation.
When the angle is small, the approximation reads
$\sin \theta \approx \theta$,
You can try this simulation below to verify the relation.
$\theta$:
Click "Try it" to display the value of each element in the form.
Result (sin$\theta$)
sin $\theta$=
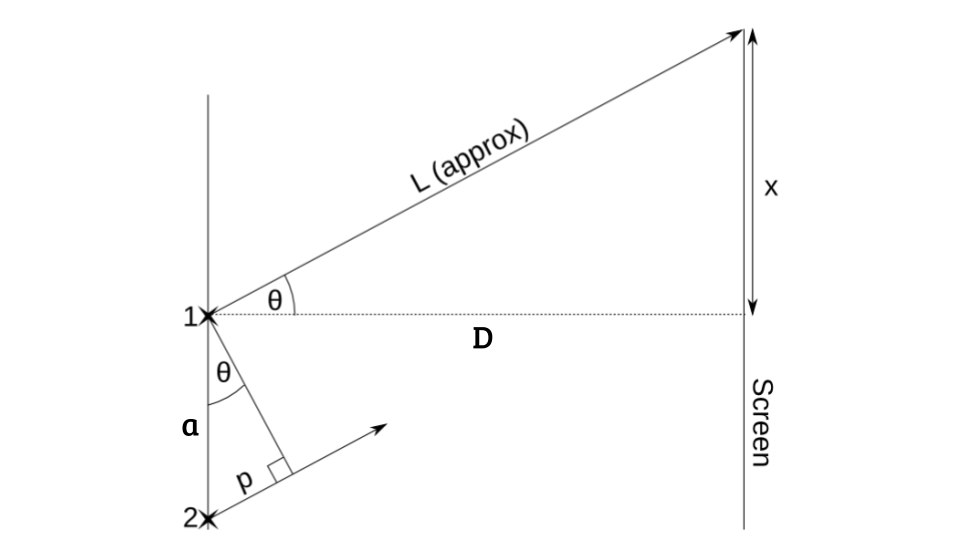
The proof of this relation can be seen from Maclaurin series, when we expand the series of $\sin(\theta)$, the result would be \begin{equation} \sin(\theta)\approx \theta -\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-... \end{equation} As you may see from there, if $\theta$ is less than 1, the second term onward would be much smaller to the point of being negligible. For instance, a $\theta$ of 0.5 would give Maclaurin expansion of \begin{align} \sin(0.5)&\approx (0.5) -\frac{0.5^3}{3!}+\frac{0.5^5}{5!}-...\\ &=0.5-0.2083-0.00026\\ &=0.479\approx 0.5 \end{align} One of the examples of this method is the derivation of $ax/D=n\lambda$. When we were able to derive until the part where $n \lambda =a \sin(\theta)$, we need to apply small angle approximation and get to $n \lambda =a \tan(\theta)$. After that, apply $\tan(\theta)=D/x$ to get to the final equation, that is $n\lambda = \frac{ax}{D}$.