Introduction to Fibonacci Numbers
The Fibonacci sequence is perhaps one of the world's most fascinating mathematical theories. It was first discovered in India, where the poets discovered that there is an organized pattern in the vedic poems. Elsewhere in the world, this sequence has seen a minor appearance in Chinese YanHui triangle (or Pascal triangle, as it is more commonly called). However, it was first clearly espoused as a mathematical theorem by Fibonacci, who was also among the pioneers to introduce Arabic numbers to the European world. Today, we found many interesting applications of the Fibonacci numbers, especially in the natural world.

Fibonacci
Imagine that you are playing a riddle with your friend, and your friend shows you this sequence of numbers and ask you to guess the next number, can you solve it? The Fibonacci sequence consists of the following infinite series of numbers: \begin{equation} 0,1,1,2,3,5,8,13,21,34,55,89,144... \end{equation} The current number is obtained by adding up the two numbers before it, for example:
- 3=2+1
- 21=13+8
- 89=55+34
Mathematical Rule of Fibonacci Number
Based on the list above, we could express the Fibonacci sequence in a set of mathematical rules. First of all, let's look at the condition:
The current number must be equal to the addition of the previous two numbers.
Based on this criterion, we can write the Fibonacci sequence as the following equation:
\begin{equation}
F_n=F_{n-1}+F_{n-2}
\end{equation}
where $n$ is the n-term of the Fibonacci numbers.
Now, let's look at the following table, which shows the list of Fibonacci numbers until $n=18$.
| $n$ | $F_n$ |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
Fibonacci Numbers and the Spiral
Now, let’s try to make 2 square blocks of the width of 1 unit, and try to stack up another square block where its width is equal to the sum of the previous 2 blocks. We would obtain the following image:
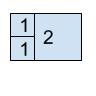
Next, we will add another square block of width 3 unit at the bottom of the 1-block and 2-block, and repeat the process until we get a square block of 8 unit. For example 5 and 8 make 13, 8 and 13 make 21, and so on.
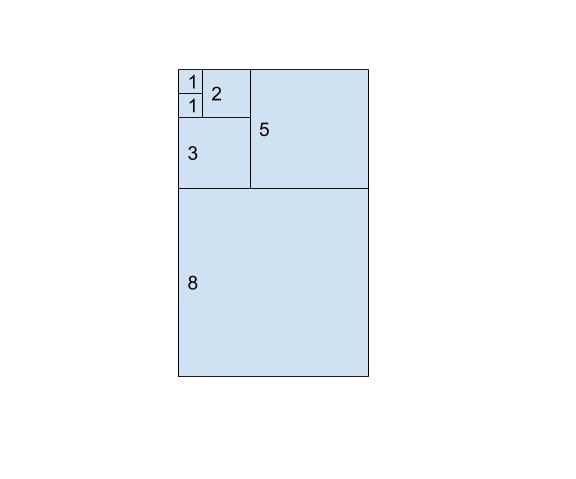
Guess what? This reminded us of the Fibonacci number! Now we try to draw a quarter-circle that encompasses each of the block in the diagram. So we will eventually get to the following:
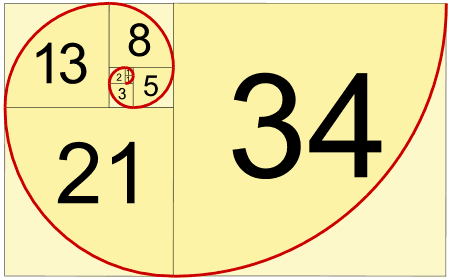
This beautiful pattern actually exists in our natural world, for examples:
Nautilus
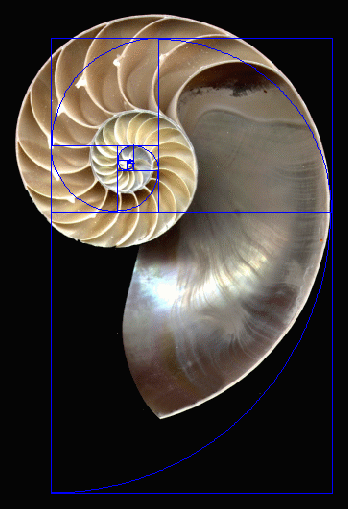
Source: https://www.goldennumber.net/wp-content/uploads/2013/08/nautilus-spiral-vs-golden-spiral.gif Hurricanes
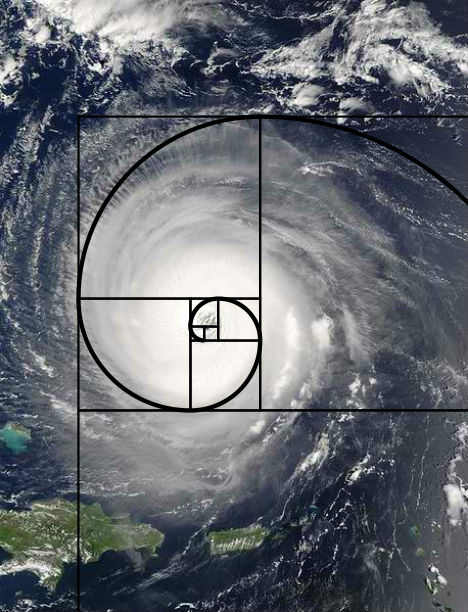
Source:http://cdn3-www.webecoist.momtastic.com/assets/uploads/2012/10/nature-geometry-hurricane1.jpg
Obtaining Golden Ratio
Now, here're some heavier stuff. When we take any two successive numbers from the Fibonacci numbers of higher term, the ratio of the number to the previous number is very close to the Golden Ratio "$\phi$" \begin{equation} \phi=\frac{1+\sqrt{5}}{2}=1.6180339... \end{equation} Now, let’s try to divide 3 with 2, apparently we would get 1.5, which is about 7% of percentage difference with the actual golden ratio number($\frac{1.6180339-1.5}{1.6180339}\approx 0.07$), not very impressive isn’t it?
But if we try to find the ratio for a pair of larger Fibonacci numbers, the result is indeed very close to the golden ratio number!
Golden Ratio
Let’s do the division of 377 and 610, we will get 1.618037, which is less than 0.0002% from the actual golden ratio. In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation, as demonstrated by the table below:
| $F_{n-1}$ | $F_n$ | $\frac{F_n}{F_{n-1}}$ |
|---|---|---|
| 2 | 3 | 1.5 |
We could write this expression in a more general form: \begin{equation} \lim_{n\rightarrow\infty}\frac{F(n+1)}{F(n)}=1.6180339.. \end{equation}
Therefore, it has been shown that Fibonacci numbers and the golden ratio are closely intertwined. Now we could use a formula that was discovered by Abraham de Moivre to calculate the Fibonacci numbers based on golden ratio: \begin{equation} x_n=\frac{\phi^n-\psi^n}{\phi-\psi}=\frac{\phi^n-\psi^n}{\sqrt{5}} \end{equation} Where $\psi=\frac{1-\sqrt{5}}{2}=-0.6180339...$ For example: \begin{equation} x_5=\frac{\phi^5-\psi^5}{\sqrt{5}} \end{equation}
Applications of Fibonacci Numbers in Genetics
Fibonacci numbers have seen a stunning occurence in the genetic studies as well. According to the genetic studies, a man has two kinds of chromosomes, X chromosome and Y chromosome; Both woman chromosomes are of the X type. The X chromosome of a man comes from his mother whereas his Y- chromosome comes from his father. For a woman, one of her X chromosome comes from her mother and another X chromosome comes from her father.
Let's take an example of man called Peter, Peter obtained his X chromosome from his mother, therefore he received his X chromosome from a single parent. His mother, however, received an X chromosome from her mother and another X chromosome from her father. Therefore, we say two grandparents contributed to Peter's X chromosome. Moving further, Peter's maternal grandfather received his X chromosome from a single parent, whereas Peter's maternal grandmother received her X chromosomes from two parents, so three great great grandparents contributed to Peter's X chromosome. Following the same logic, there are 5 great great grandparents who contributed to the male descendant's X chromosome.
Readers with sharp eyes will see that all the numbers of ancestors for a particular generation follow the Fibonacci numbers, as shown in the diagram below.